4892. Replacement

Given a sequence of n positive integers. You must replace each element with the next nearest one (with a larger index) that is strictly larger than its value. If there is no larger element, replace this element with zero.

Input. First line contains the number of elements n (1 ≤ n ≤ 10⁵). Second line contains n positive integers a_i (a_i ≤ 10⁹) – the values of sequence elements.

Output. Print the desired sequence, separating the neighboring elements with a single space.

Sample input 1	Sample output 1
6 1 2 3 1 1 5	2 3 5 5 5 0
Sample input 2	Sample output 2
5 1 2 3 4 5	2 3 4 5 0

SOLUTION

set data structure

Algorithm analysis

Let the numbers of the input sequence a₁, a₂, …, a_n correspond to the heights of houses located next to each other. For example, the first test can be depicted as follows:

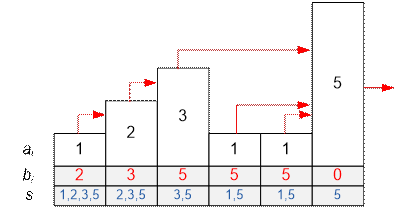
Let b₁, b₂, …, b_n be the resulting array. Then b_i equals to such a_j that if you look at the end of the i-th house to the left, then the house a_j will be the closest visible one. Obviously that b_n = 0.

Let’s process the houses from right to left. Let a_i be the current house under consideration. Let’s keep the set s of house heights visible from the left end of the i-th house (including a_i). Then b_i equals to the second element of the set s.

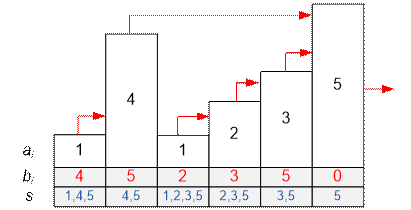
Consider how to maintain a set of s when adding a new house. We move from right to left, let the third house with height a₃ = 1 have already been considered. The current set equals to s = {1, 2, 3, 5}. We process the second house with height a₂ = 4. Obviously, it will overlap the left view of all houses, no more than its height. Add the value a₂ = 4 to the set s, and then remove from s all numbers less than a₂ = 4 (you can use the erase method for the interval). After the described operations, the set will take the form s = {4, 5}.

Algorithm realization

Declare a set s and an iterator it onto it. Store the input and output sequences in arrays in and out.

#define MAX 100001

set<int> s;

set<int>::iterator it;

int in[MAX], out[MAX];

Read the input array.

scanf("%d",&n);

for(i = 0; i < n; i++)

scanf("%d",&in[i]);

Process the houses from right to left.

for(i = n - 1; i >= 0; i--)

{

Insert the height of the current house into the set.

s.insert(in[i]);

Look for the position of the inserted house of height in_i. Remove from the set s all heights less than in_i.

it = s.find(in[i]);

s.erase(s.begin(),it);

Print the second element of the set. If it doesn't exist, print 0.

it++;

if(it == s.end())

out[i] = 0;

else

out[i] = *it;

}

Print the resulting array.

for(i = 0; i < n; i++)

printf("%d ",out[i]);

printf("\n");